Le moteur d'inférence
Le moteur d'inférence interprète cycliquement la base de règles en fonction de la base de faits. L’interprétation consiste à évaluer l'adéquation des règles avec la base de faits, à sélectionner la meilleure pour chaque type et à les appliquer. En fonction de leurs évaluations, de leurs sélections et éventuellement de leurs récompenses, le moteur d'inférence réévalue la pertinence des règles qui ne seraient pas au maximum puis élimine celles qui seraient en dessous d'un seuil minimum autorisé.
Toutes les règles suivent exactement le même traitement, sauf les règles de récompense et les règles de contrôle.
L'évaluation des règles
L'évaluation d'une règle consiste à évaluer la crédibilité d'une règle à être appliquée en fonction des événements de la base de faits. Plus précisément, la crédibilité représente le degré d’appariement entre une règle et le contenu de la mémoire événementielle. La crédibilité est bornée entre 0, une correspondance, et 1, une correspondance parfaite. Une règle avec une crédibilité nulle ne peut être sélectionnée.
La première étape dans l'évaluation des règles consiste à vérifier, si la base de faits offre au moins un nombre d'évènements correspondant aux prémisses excitatrices de la règle (même type, même signe pour l'indice temporel). Un évènement ne peut satisfaire deux prémisses à la fois. Même si toutes les tolérances d'une prémisse sont à l'infini, la présence d'un événement correspondant reste évidemment obligatoire. Dans le cas où il manque un événement pour évaluer la condition excitatrice, la crédibilité est nulle.
Dans le cas contraire, la seconde étape consiste à calculer le score de la condition excitatrice et celui de la condition inhibitrice . A noter que les calculs des scores représentent des distances entre les composantes de la condition et celles des événements idoines, il est considéré que chaque composantes est statistiquement indépendante des autres, même en ce qui concerne les composantes d'entrées. Aussi, il est conseillé de s'assurer de l'indépendance statistique des entrées.
Le calcul de la crédibilité s'effectuera de la manière suivante :
Si le score inhibiteur est supérieur au score excitateur alors la crédibilité est nulle.
Le score de la condition excitatrice
Les prémisses de la condition excitatrice sont considérées comme conjonctives. La distance de la condition excitatrice vis à vis de la base de faits correspond alors à la multiplication des distances des prémisses vis à vis d'un événement.
Plus précisément, le score de la condition excitatrice revient à rechercher l’appariement qui minimise la distance entre les événements et les prémisses dans leur ensemble. Toutes les composantes sont évaluées, indice temporel, crédibilité, information, vecteur d’entrée.
Pour une configuration d'appariement possible entre les évènements de la base de faits et les prémisses de la condition excitatrice, l’appariement entre prémisses ayant noyaux gaussiens (moyenne avec un écart type ) et événements de type idoines s’exprime de la manière suivante :
Lorsque l'écart type d'une composante est nul, si la composante idoine de l'évènement est égale à alors cela revient à multiplier par 1, sinon cela revient à multiplier par 0.
Le score de la condition excitatrice correspond à l'appariement le plus avantageux soit, pour une configuration de la mémoire événementielle à l'interprétation :
Le score de la condition inhibitrice
Les prémisses de la condition inhibitrice sont considérées disjonctives. La distance de la condition inhibitrice avec la base de faits correspond à la somme des distances entre les prémisses inhibitrices avec l'évènement le plus en adéquation. Ainsi, l’appariement entre prémisses ayant noyaux gaussiens (moyenne avec un écart type ) et événements de type idoines s’exprime de la manière suivante :
Le score de la condition inhibitrice correspond à l'appariement le plus avantageux soit, pour une configuration de la mémoire événementielle à l'interprétation :
Remarque sur le calcul de la distance
La sensibilité
La sensibilité du calcul numérique du score dépend de l'implémentation. Dans la version standard, lorsque le score devient inférieur à , il est considéré comme nul.
La propagation de la crédibilité
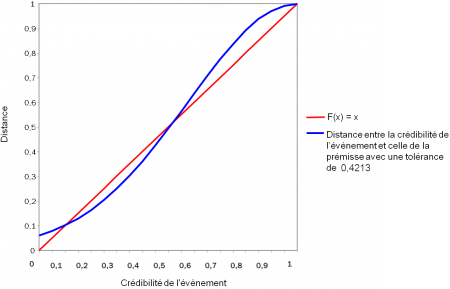
Concernant plus particulièrement la crédibilité, dans le cas où il serait souhaité que la valeur de crédibilité d'un évènement serve à pondérer le calcul d'un score, il faut que la distance entre crédibilités approxime la valeur de la crédibilité de l'évènement. Cela revient à déterminer dans une prémisse la moyenne et l'écart type de la composante dédiée à la crédibilité qui approxime au mieux la fonction d'identité, soit :
Une recherche par dichotomie évalue la composante optimale avec une moyenne et un écart type . La figure ci-dessous illustre la courbe des distances obtenues avec ces valeurs et la fonction identité à titre de comparaison.
La sélection des règles
Le moteur d'inférence sélectionne, pour chaque type, la règle la plus adéquate parmi d’autres règles en fonction de leur niveau de spécialisation. La méthode utilisée consiste à sélectionner la règle qui maximise la vraisemblance, c'est-à-dire la règle possédant l’espérance maximale. Lorsqu’une règle est sélectionnée, un ajustement de sa condition peut s’effectuer.
L'espérance et la spécificité
L’espérance d’une règle parmi règles avec leur spécificité avec leur crédibilité à l’interprétation s’écrit :
La valeur de l'espérance d'une règle est comprise entre 0 et 1, borne incluse.
La spécificité d’une règle se calcule à l’aide de l’ensemble des variances des composantes des prémisses excitatrices :
Cependant, ce calcul pose problème de deux manières. Premièrement, aux limites avec des variances tendant vers zéro ou l'infini, ce calcul ne trouve pas de solution analytique. Secondement, ce calcul ne sert de comparaison uniquement pour les conditions de règles de même taille.
Le premier problème est résolu empiriquement en posant comme valeur minimale (assimilée à zéro) de la variance et comme valeur maximale (assimilée à l'infini) .
Le second problème est résolu en rajoutant des prémisses avec des tolérances infinies de sorte que toutes les conditions possèdent un même nombre de prémisses et en rajoutant à chaque prémisse une tolérance nulle () ou infini () représentant la nécessité ou non d'une correspondance avec un événement. Compte tenu de la structure des conditions des règles, les prémisses rajoutées sont uniquement des prémisses capturant des événements internes possédant donc que trois composantes (crédibilité, information, indice temporel) et une tolérance à .
Ainsi, en considérant une condition d'une règle avec prémisses regroupant composantes dans un système décisionnel autorisant un maximum de prémisses par condition, la spécificité prend la forme suivante :
Pour un type de règle, la règle sélectionnée en fonction de l'état de la mémoire évènementielle à l’interprétation correspond à celle qui maximise l’espérance :
Dans le cas où l'espérance maximale est nulle, aucune règle n'est sélectionnée.
Si plusieurs règles avancent la même espérance maximale, c'est la règle avec la plus grande spécificité calculée sur les prémisses inhibitrices qui l'emporte. Dans le cas où la spécificité serait identique, ce sera la première règle évaluée avec l'espérance maximale qui sera sélectionnée. L'ordre d'évaluation des règles ne change pas au cours des cycles d'interprétation.
L'ajustement des prémisses
En cas de sélection, une règle peut ajuster sa condition de façon à optimiser son espérance. Seules les prémisses excitatrices peuvent faire l'objet d'un ajustement.
Chacune des règles possède un nombre maximal d'ajustements qui est fixé à l'initialisation. En effet, chaque règle comporte un nombre d’ajustement maximal afin d’optimiser l’espérance de la règle. Le calcul de l'ajustement s'effectue sur toutes les composantes dont la tolérance est ni nulle ni infinie. L'ajustement des composantes s'appuie sur l’hypothèse de leurs indépendances statistiques. Un noyau gaussien d'une composante est alors ajusté de la manière suivante à la énième sélection de la règle, avec les valeurs des événements :
Par ailleurs, l'ajustement de la variance oblige le recalcul de la spécificité de la règle.
La pertinence des règles
Les règles susceptibles d'être oubliées doivent justifier de leur pertinence à être présentes dans la base de règles.
La pertinence d’une règle reflète son activité et son originalité. L’évolution de la pertinence d’une règle repose sur des renforcements positifs et négatifs successifs. La dynamique de la pertinence discrimine les règles pertinentes de celles qui sont redondantes ou inactives. Toutefois, la dynamique prend en compte le fait qu’une règle ayant été suffisamment pertinente puisse être conservée bien qu’elle soit inappropriée pendant un certain temps.
Les récompenses positives proviennent soit de la sélection, soit d'une règle de récompense. Les récompenses négatives proviennent uniquement de la redondance et de l'inactivité. Il n'y a pas de récompense négative. Une bonne règle correspond à une règle dont l’efficacité est garantie par la condition. Une récompense positive permet identifier les règles efficaces bien qu'elles soient peu usitées. Une règle qui ne serait pas toujours efficace est soit éliminée par la création d'une règle plus spécifique, soit inhibée par une nouvelle règle dans le contexte où elle ne serait pas adaptée. Dans le cas où le contexte pertinent de la règle reste général, la règle est maintenue.
La pertinence correspond à un réel compris entre 0 et 1, 0 indiquant une règle non pertinente. Une pertinence à 1 signifie que la règle sera toujours pertinente, soit qu’elle restera toujours avec une pertinence maximale. Après chaque cycle d'interprétation, les règles ayant une pertinence en dessous du seuil d'oubli sont éliminées.
Dans le cas théorique d’une pertinence évaluée en continue , la dynamique se traduit par une équation différentielle basée sur le renforcement positif et négatif :
Renforcer la pertinence positivement ou négativement en fonction de la pertinence permet de rendre les règles de faible pertinence sensibles aux renforcements positifs et les règles de forte pertinence moins sensibles aux renforcements négatifs.
Quatre sortes de renforcement existent : la taxe, l’enchère, le remboursement et, la récompense. La taxe et l’enchère produisent des renforcements négatifs, le remboursement et la récompense produisent des renforcements positifs. Les équations qui suivent traduisent le cas discret de la dynamique de la pertinence à chaque cycle d'interprétation . Les taux présentés ci-dessous correspondent à des constantes appartenant aux paramètres du système décisionnel.
La taxe
A chaque n interprétation, toutes les règles subissent une taxe qui vient éroder leur pertinence selon un taux négatif . Cette taxe permet de diminuer jusqu’au seuil d’oubli les règles qui ne reçoivent aucun renforcement positif. La au cycle d'interprétation se calcule en fonction de la pertinence précédente :
L’enchère
Le rôle de l’enchère consiste à diminuer la pertinence de toutes les règles redondantes selon un taux négatif . A chaque interprétation, les règles paient une enchère proportionnelle à leur espérance . La de l’enchère au cycle d'interprétation est calculée en fonction de la pertinence :
Le remboursement
L’enchère pénalisant davantage les règles possédant les espérances les plus élevées, il est nécessaire de rembourser la mise de règle sélectionnée. Ce remboursement s’effectue selon un taux positif proportionnellement à l’espérance de la règle sélectionnée . Le au cycle d'interprétation se calcule en fonction de la pertinence précédente :
La récompense
La récompense déclenchée par l’arrivée d’un événement de récompense augmente la pertinence des règles ciblées en fonction de leur pertinence. Le mécanisme ciblant indirectement les règles à récompenser est présenté avec la base de règles. La récompense est proportionnelle à la crédibilité portée par l'évènement de récompense et avec un taux positif . Le produit par la récompense au cycle d'interprétation se calcule en fonction de la pertinence précédente :
Les quatre situations possibles
A partir de ces quatre sources, quatre situations de calcul de la pertinence se profilent au cycle d'interprétation : La première situation correspond aux règles qui n’ont été ni sélectionnées ni récompensées, la réévaluation de leur pertinence revient à : La deuxième situation concerne le cas où la règle est sélectionnée : La troisième situation survient lorsque la règle non sélectionnée reçoit une récompense : La dernière situation arrive quand la règle sélectionnée est en même temps récompensée :
Les cas particuliers
Les règles de récompense
Les règles de récompense ne peuvent être la cible de récompense. En revanche, une règle de récompense s'auto-rétribue à chaque sélection de la même manière que les autres règles ciblées par la récompense.
Autrement dit, le calcul de la pertinence repose uniquement sur les équations décrites dans le cadre de la première et de la dernière situation présentées ci-dessus.
L'idée est qu'une règle un peu activée mais ne récompensant que peu les règles visées possède une faible utilité à terme, et à l'inverse, une règle peu usitée mais récompensant fortement les règles ciblées doit être maintenue.
Les règles de contrôle
Compte tenu que les règles de contrôle évaluent la base de faits dans la durée, le traitement des règles de contrôle diffère des autres catégories de règles. Le rôle des règles de contrôle est présenté dans la partie abordant la base de connaissances.
En effet, la première sélection d'une règle de contrôle repose uniquement sur l'adéquation des prémisses de prédiction et de marquage. Ensuite, tant que la prémisse de prédiction est satisfaite, à chaque cycle d'interprétation, les autres règles de contrôle du même type sont inhibées et le calcul de la crédibilité de la règle s'effectue de la même manière que les autres catégories de règles.
Au final la crédibilité de la règle de contrôle sur cycle d'interprétation correspond à la crédibilité maximale :
L'ajustement de la règle s'effectue uniquement sur l'indice temporel de la prémisse de marquage et avec l'évènement maximisant la crédibilité de la règle de contrôle. Par ailleurs, l'ajustement est alors reporté à la conclusion de la règle de prédiction.
Le calcul de l'ajustement est quasiment le même que pour les règles d'autres catégories sauf lorsque l'indice temporel de l’évènement devient trop petit par rapport à la couverture de l'évaluation de la prédiction.
En effet, l'évaluation de la prédiction est asymétrique puisqu'elle s'effectue avec la couverture sur l'intervalle . Afin de minimiser le risque de dérive, les valeurs inférieures à ne participent pas à l’estimation de la moyenne mais contribuent à deux fois à celle de la variance pour tenir compte la valeur symétrique :
Concernant la dynamique de la pertinence des règles de contrôle, la taxe est prélevée à chaque cycle d'interprétation, l'enchère et le remboursement sont appliqués lors de la première sélection avec une espérance à 1 ; lorsqu'elle n'est pas sélectionnée l'espérance est à 0. Dans le cas où la règle de prédiction et celle de marquage associée à la règle de contrôle possèdent également des conditions exclusives avec les autres règles, elles ont une pertinence identique à un cycle d'interprétation près.